基于模糊神经混合系统的自适应控制方法及其应用
模糊逻辑系统与神经网络的结合形式随着研究角度和应用领域不同而有所不同,在这类系统中,系统本质上还是模糊逻辑系统结构,但是可以把模糊逻辑系统看作具有网络化的结构,直接利用神经网络的学习能力与映射能力来获得模糊逻辑系统的参数或具体结构,从而使模糊逻辑系统具有自学习和自适应能力,该过程并不改变模糊系统所具有的模糊化、解模糊化和模糊推理的功能,而是利用神经网络实现隶属函数、模糊规则的数字化处理,实现“模糊化-模糊推理-解模糊化”整个过程的“网络化”,也可以用神经网络学习或聚类的方法从输入输出数据中获取规则,然后在性能指标指导下,对规则进行调整,从而使模糊系统具有规则的自组织能力[1]。
在另外一个范畴内,可以将模糊逻辑系统与神经网络根据不同的功能、用途集成在一个系统里,模糊逻辑系统与神经网络技术在这类系统中各自发挥自己的功能,利用各自的优势为实现共同的目标而实现功能结合与互补,这类模糊逻辑系统与神经网络结合的方法称之为模糊神经混合系统FNHS(Fuzzy-Neural Hybrid System)[2]。
从控制角度而言,神经网络自适应控制包括直接自适应控制和间接自适应控制。间接自适应控制通常由控制器和模型两部分组成。在线辨识模型,并通过模型在线调整神经网络控制器间接自适应控制,具有良好的适应性[3]。但是,在线辨识被控对象的模型存在运算量大、控制精度低等问题,对不可重复过程与时变动力学系统训练困难,在实际工程控制中实用性不大。直接自适应控制是根据过程的输出信息来控制优化参数,不需要预先知道系统动力学特征或在线辨识的模型,这也正是传统的自适应控制所不能解决的问题。这种控制器是直接根据控制精度设计,不需要经过事先训练,也不依赖于对象的辨识模型,具有良好的动态响应性能和稳态精度,网络权值的调整是随时间关系的自适应收敛过程,常用的基于神经网络的自适应控制方式为直接逆控制、模型网络参考控制。但是,这2种控制方式都存在着较大的计算量和辨识的问题,而且对于直接逆控制,如果系统的逆不存在了,该方法就会失效。
基于模糊神经混合系统的自适应控制(FANNC)结合了神经网络直接自适应控制的特点,结构如图1所示。由1个反馈控制器(FC)、1个神经网络控制器(NNC)和模糊推理机(FIE)组成[4]。
2 基于模糊神经混合系统的自适应控制器的设计
分目标学习误差由模糊推理机的一组模糊规则给出,如表1所示。表中符号PB、PM、PS、0、NS、NM、NB分别表示正大、正中、正小、零、负小、负中、负大等概念[5]。表中模糊关系不再是传统意义上的模糊控制策略,而是每一控制周期中用于NNC训练的分目标学习误差。NNC在学习过程中,逐步跟踪系统的逆动力学,并产生一个自适应控制信号,使系统输出跟踪给定的参考信号消除的不再单纯是系统的输出误差,而是误差和误差变化的综合影响,从而避免了反馈误差学习法可能造成的NNC的输出产生振荡或进入饱和状态等问题。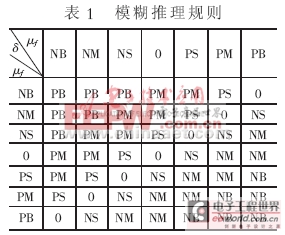
为实现上述模糊推理规则,必须对模糊推理机FIE的输入变量进行模糊化处理,即将输入变量从基本论域转化到相应的模糊论域。为此,引入反馈控制器FC输出变量μf及其变化变量μf的量化因子Kμf,Kμf。假定变量μf的基本论域为(-nfm,nfm),模糊论域分别为(-nμf,-nμf+1,…0,…,nμf-1,nμf),变量nf的基本论域为(-nfm,nfm),模糊论域分别为(-nμf,-nμf+1,…0,…,nμf-1,nμf),则量化因子Kμf,Kμf可由下式确定:


模糊变量Uf(k)、f(k)的论域、模糊子集及其隶属函数的定义如图2所示。为改善模糊推理机的输出特性,FIE输出变量δ论域、模糊子集及其隶属函数的定义如图3所示[6]。当系统偏差较大时,模糊集隶属函数分辨率较低,FIE输出变化比较缓慢可以保证NNC的学习比较平稳。

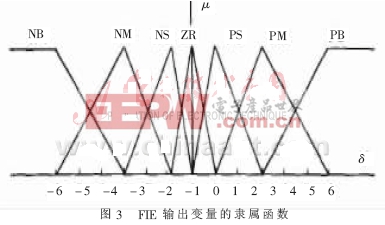
在控制过程中,系统根据每一采样时刻FC的输出信号及其变化,由图2确定各模糊集的隶属度,然后利用模糊推理规则如表1所示,图3确定输出变量所有可能的模糊截集。并以重心发模糊判决,得到分目标学习误差 ,式中离散计算步长的取值大小可能影响模糊判决的精度。
,式中离散计算步长的取值大小可能影响模糊判决的精度。



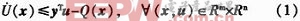

评论